qml.fourier¶
Overview¶
This module contains functions to analyze the Fourier representation of quantum circuits.
Functions¶
|
Compute the frequency spectrum of the Fourier representation of simple quantum circuits ignoring classical preprocessing. |
|
Computes the first 2d+1 Fourier coefficients of a 2π periodic function, where d is the highest desired frequency (the degree) of the Fourier spectrum. |
|
Extract the frequencies contributed by an input-encoding gate to the overall Fourier representation of a quantum circuit. |
|
Join two sets of frequencies that belong to the same input. |
|
Compute the frequency spectrum of the Fourier representation of quantum circuits, including classical preprocessing. |
|
Reconstruct an expectation value QNode along a single parameter direction. |
Visualization¶
Tools to visualize the Fourier representations can be found in the fourier.visualize
submodule. This requires the matplotlib package to be installed.
|
Plot a set of Fourier coefficients as a bar plot. |
|
Plot a list of sets of Fourier coefficients as a box plot. |
|
Plot a list of sets of coefficients in the complex plane for a 1- or 2-dimensional function. |
|
Plot a list of sets of Fourier coefficients on a radial plot as box plots. |
|
Plots a list of sets of Fourier coefficients as a violin plot. |
Fourier representation of quantum circuits¶
Consider a quantum circuit that depends on a parameter vector x with length N. The circuit involves application of some unitary operations U(x), and then measurement of an observable ˆO. Analytically, the expectation value is
This output is simply a function f(x)=⟨ψ(x)|ˆO|ψ(x)⟩. Notably, it is a periodic function of the parameters, and it can thus be expressed as a multidimensional Fourier series:
where ni are integer-valued frequencies, Ωi are the set of available values for the integer frequencies, and the cn1,…,nN are Fourier coefficients.
As a simple example, consider simple_circuit below, which is a function of a
single parameter.
import pennylane as qml
from pennylane import numpy as np
dev = qml.device('default.qubit', wires=2)
@qml.qnode(dev)
def simple_circuit(x):
qml.RX(x[0], wires=0)
qml.RY(x[0], wires=1)
qml.CNOT(wires=[1, 0])
return qml.expval(qml.PauliZ(0))
We can mathematically evaluate the expectation value of this function to be ⟨Z⟩=0.5+0.5cos(2x). Thus, the Fourier coefficients of this function are c0=0.5, c1=c∗−1=0, and c2=c∗−2=0.25.
The PennyLane fourier module enables calculation of
the values of the Fourier coefficients cn1,…,nN.
Knowledge of the coefficients, and thereby the spectrum of frequencies
where the coefficients are non-zero, is important
for the study of the expressivity of quantum circuits, as described in Schuld,
Sweke and Meyer (2020) and Vidal and
Theis, 2019 – the more coefficients
available to a quantum model, the larger the class of functions that model can
represent, potentially leading to greater utility for quantum machine learning
applications.
Calculating the frequencies supported by a circuit¶
For certain circuits, information on the frequency spectra Ωj can be derived solely from the structure of the gates that encode the corresponding inputs xj (see for example Schuld, Sweke, and Meyer (2020)). More precisely, if all input-encoding gates are of the form e−ixjG, where G is a Hermitian operator that “generates” the operation, we can deduce a maximum set of frequencies that can theoretically appear in Ωj. Depending on the non-input-encoding gates in the circuit, some of these theoretically supported frequencies may end up having vanishing Fourier coefficients, and Ωj effectively turns out to be smaller. However, estimates based on the input-encoding strategy can still be useful to understand the potential expressivity of a type of ansatz.
The theoretically supported frequencies can be computed
using the circuit_spectrum() function. To mark which gates encode
inputs (and, for example, which ones are only used for trainable parameters), we
have to give input-encoding gates an id:
import pennylane as qml
dev = qml.device('default.qubit', wires=2)
@qml.qnode(dev)
def simple_circuit_marked(x):
qml.RX(x[0], wires=0, id="x")
qml.RY(x[0], wires=1, id="x")
qml.CNOT(wires=[1, 0])
return qml.expval(qml.PauliZ(0))
We can then compute the frequencies supported by the input-encoding gates as:
>>> from pennylane.fourier import circuit_spectrum
>>> freqs = circuit_spectrum(simple_circuit_marked)([0.1])
>>> for k, v in freqs.items():
>>> print(k, ":", v)
x : [-2.0, -1.0, 0.0, 1.0, 2.0]
Note
Some encoding-gate types may give rise to non-integer-valued frequencies. In this case,
the circuit_spectrum() function computes the frequency sets Ωj
of the Fourier sum of the form
with ω∈R. Just like any other function, such a sum can be turned into a proper Fourier series, but the mapping from non-integer-valued to integer-valued frequencies is not always trivial.
Calculating the Fourier coefficients¶
To get a more accurate picture of the Fourier series representation of a quantum circuit,
we have to compute the Fourier coefficients cn1,…,nN. This is done using numerical methods in the
coefficients() function:
>>> from pennylane.fourier import coefficients
>>> coeffs = coefficients(simple_circuit, 1, 2)
>>> print(np.round(coeffs, decimals=4))
[0.5 +0.j 0. -0.j 0.25+0.j 0.25+0.j 0. -0.j]
The inputs to the coefficients() function are
A function, or QNode containing the variational circuit for which to compute the Fourier coefficients,
the length of the input vector, and
the maximum frequency for which to calculate the coefficients (also known as the degree).
Internally, the coefficients are computed using NumPy’s discrete Fourier
transform
function. The order of the coefficients in the output thus follows the standard
output ordering, i.e., [c0,c1,c2,c−2,c−1], and similarly
for multiple dimensions. The normalization convention used here corresponds to
the norm="forward" option in the NumPy transforms, i.e., the Fourier
transform over an array of size N is rescaled by 1/N, while the
inverse Fourier transform is left as-is.
For more details and examples of coefficient calculation, please see the
documentation for coefficients().
Fourier coefficient visualization¶
A key application of the Fourier module is to analyze the expressivity of classes of quantum circuit families. The set of frequencies in the Fourier representation of a quantum circuit can be used to characterize the function class that a parametrized circuit gives rise to. For example, if an embedding leads to a Fourier representation with a few low-order frequencies, a quantum circuit using this embedding can only express rather simple periodic functions.
The Fourier module contains a number of methods to visualize the coefficients of the Fourier series representation of a single circuit, as well as distributions over Fourier coefficients for a parametrized circuit family.
Note
Visualization of the Fourier coefficients requires the matplotlib
library. As such, visualization functions are contained in the submodule
pennylane.fourier.visualize. The visualization functions are structured
to accept matplotlib axes as arguments so that additional configuration
(such as adding titles, saving, etc.) can be done outside the functions. Many
of the plots, however, require a specific number of subplots. The examples
below demonstrate how the subplots should be created for each function.
Visualizing a single set of coefficients¶
While all the functions available for visualizing multiple sets of Fourier
coefficients can be used for a single set, the primary tool for this purpose is
the bar() function. Using the coefficients we obtained in the
earlier example,
>>> from pennylane.fourier.visualize import *
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(2, 1, sharex=True, sharey=True) # Set up the axes
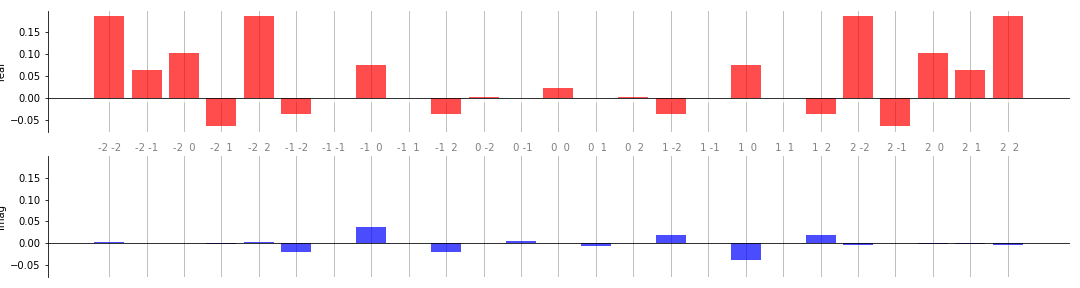
>>> bar(coeffs, 1, ax)

In the bar plots, real coefficients are shown in the top panel, and complex in
the bottom. The labels along the x-axis represent the coefficient frequencies
(for large plots, it is sometimes convenient to remove these by passing
show_freqs=False to the plotting function).
Below is a more complex example that demonstrates some of the additional customization options available:
from functools import partial
weights = np.array([[0.1, 0.2, 0.3], [0.4, 0.5, 0.6]])
@qml.qnode(dev)
def circuit_with_weights(w, x):
qml.RX(x[0], wires=0)
qml.RY(x[1], wires=1)
qml.CNOT(wires=[1, 0])
qml.Rot(*w[0], wires=0)
qml.Rot(*w[1], wires=1)
qml.CNOT(wires=[1, 0])
qml.RX(x[0], wires=0)
qml.RY(x[1], wires=1)
qml.CNOT(wires=[1, 0])
return qml.expval(qml.PauliZ(0))
coeffs = coefficients(partial(circuit_with_weights, weights), 2, 2)
# Number of inputs is now 2; pass custom colours as well
fig, ax = plt.subplots(2, 1, sharex=True, sharey=True, figsize=(15, 4))
bar(coeffs, 2, ax, colour_dict={"real" : "red", "imag" : "blue"})
Visualizing multiple sets of coefficients¶
Suppose we do not want to visualize the Fourier coefficients for a fixed
weights argument in circuit_with_weights, but the distribution over sets
of Fourier coefficients when the weights are randomly sampled. For each
weights sample we get a different set of coefficients:
coeffs = []
for _ in range(100):
weights = np.random.normal(0, 1, size=(2, 3))
c = coefficients(partial(circuit_with_weights, weights), 2, degree=2)
coeffs.append(np.round(c, decimals=8))
One option to plot the distribution is violin():
fig, ax = plt.subplots(2, 1, sharey=True, figsize=(15, 4))
violin(coeffs, 2, ax, show_freqs=True)

A similar option is box(), which
produces a plot of the same format but using a box plot.
A different view can obtained using the
radial_box() function. This “rolls up”
the coefficients onto a polar grid. Let us use it to visualize the same set of
coefficients as above:
# The subplot axes must be *polar* for the radial plots
fig, ax = plt.subplots(
1, 2, sharex=True, sharey=True,
subplot_kw=dict(polar=True),
figsize=(15, 8)
)
radial_box(coeffs, 2, ax, show_freqs=True, show_fliers=False)
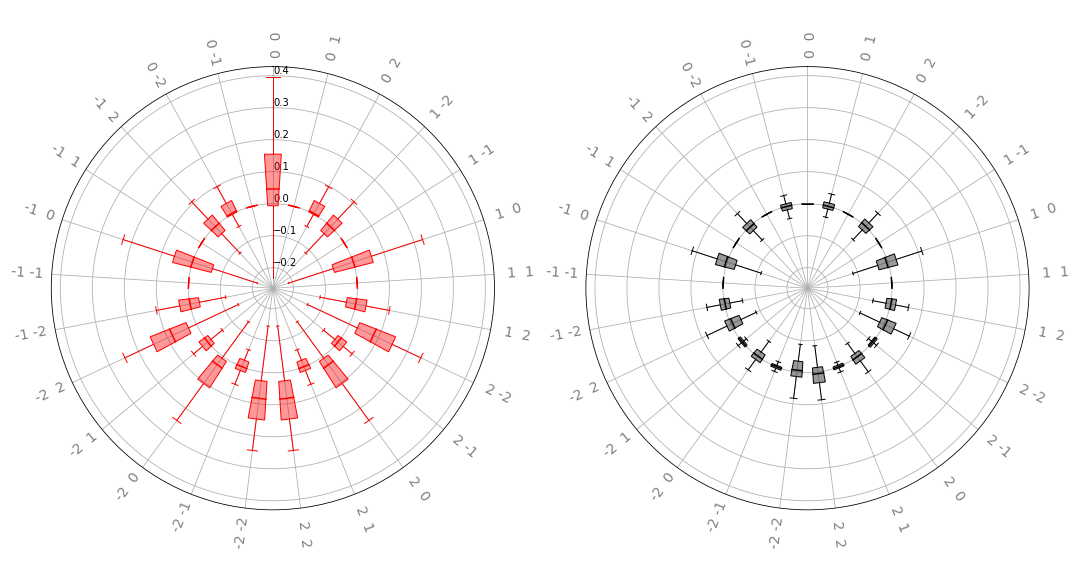
The left plot displays the real part, and the right the imaginary
part of the distribution over a parametrized quantum circuit’s
Fourier coefficients. The labels on the “spokes” of the wheels represent the particular
frequencies; we see that this matches the coefficients we found earlier. Note
how the coefficient c0 appears in the top middle of each plot; the
negative frequencies extend counterclockwise from that point, and the positive
frequencies increase in the clockwise direction. Such plots allow for a more
compact representation of a large number of frequencies than the linear violin
and box plots discussed above. For a large number of frequencies, however, it is
recommended to disable the frequency labelling by setting show_freqs=False,
and hiding box plot fliers as was done above.
Finally, for the special case of 1- or 2-dimensional functions, we can use the
panel() function to plot the distributions of the
sampled sets of Fourier coefficients on the complex plane.
# Need a grid large enough to hold all coefficients up to frequency 2
fig, ax = plt.subplots(5, 5, figsize=(12, 10), sharex=True, sharey=True)
panel(coeffs, 2, ax)
