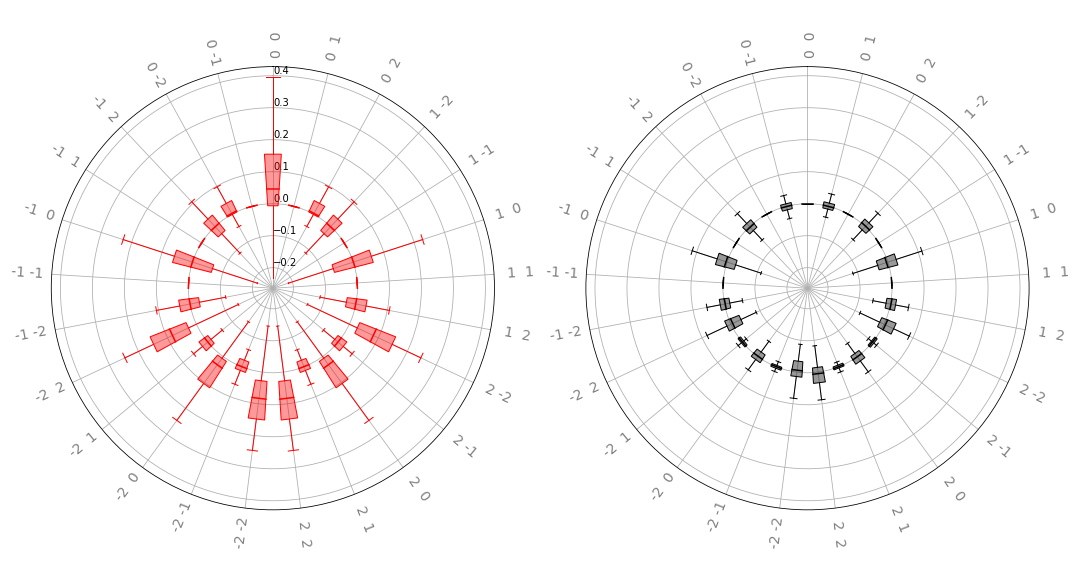
qml.fourier.visualize.radial_box¶
- radial_box(coeffs, n_inputs, ax, show_freqs=True, colour_dict=None, show_fliers=True)[source]¶
Plot a list of sets of Fourier coefficients on a radial plot as box plots.
Produces a 2-panel plot in which the left panel represents the real parts of Fourier coefficients. This method accepts multiple sets of coefficients, and plots the distribution of each coefficient as a boxplot.
- Parameters:
coeffs (list[array[complex]]) – A list of sets of Fourier coefficients. The shape of the coefficient arrays should resemble that of the output of numpy/scipy’s
fftnfunction, orcoefficients().n_inputs (int) – Dimension of the transformed function.
ax (array[matplotlib.axes.Axes]) – Axes to plot on. For this function, subplots must specify
subplot_kw={"polar":True}upon construction.show_freqs (bool) – Whether or not to label the frequencies on the radial axis. Turn off for large plots.
colour_dict (dict[str, str]) – Specify a colour mapping for positive and negative real/imaginary components. If none specified, will default to:
{"real" : "red", "imag" : "black"}showfliers (bool) – Whether or not to plot outlying “fliers” on the boxplots.
merge_plots (bool) – Whether to plot real/complex values on the same panel, or on separate panels. Default is to plot real/complex values on separate panels.
- Returns:
The axes after plotting is complete.
- Return type:
array[matplotlib.axes.Axes]
Example
Suppose we have the following quantum function:
dev = qml.device('default.qubit', wires=2) @qml.qnode(dev) def circuit_with_weights(w, x): qml.RX(x[0], wires=0) qml.RY(x[1], wires=1) qml.CNOT(wires=[1, 0]) qml.Rot(*w[0], wires=0) qml.Rot(*w[1], wires=1) qml.CNOT(wires=[1, 0]) qml.RX(x[0], wires=0) qml.RY(x[1], wires=1) qml.CNOT(wires=[1, 0]) return qml.expval(qml.Z(0))
We would like to compute and plot the distribution of Fourier coefficients for many random values of the weights
w. First, we generate all the coefficients:from functools import partial coeffs = [] n_inputs = 2 degree = 2 for _ in range(100): weights = np.random.normal(0, 1, size=(2, 3)) c = qml.fourier.coefficients(partial(circuit_with_weights, weights), n_inputs, degree) coeffs.append(c)
We can now plot by setting up a pair of
matplotlibaxes and passing them to the plotting function. Note that the axes passed must use polar coordinates.import matplotlib.pyplot as plt fig, ax = plt.subplots( 1, 2, sharex=True, sharey=True, subplot_kw={"polar": True}, figsize=(15, 8) ) qml.fourier.visualize.radial_box(coeffs, 2, ax, show_freqs=True, show_fliers=False)