qml.operation

This module contains the abstract base classes for defining PennyLane operations and observables.

Warning

Unless you are a PennyLane or plugin developer, you likely do not need to use these classes directly.

See the main operations page for details on available operations and observables.

Description

Qubit Operations

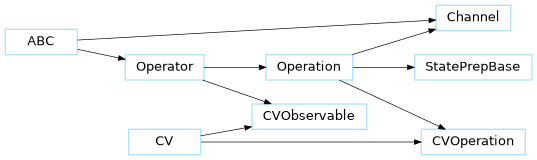
The Operator class serves as a base class for operators, and is inherited by both the Observable class and the Operation class. These classes are subclassed to implement quantum operations and measure observables in PennyLane.

• Each Operator subclass represents a general type of map between physical states. Each instance of these subclasses represents either

  • an application of the operator or

  • an instruction to measure and return the respective result.

  Operators act on a sequence of wires (subsystems) using given parameter values.

• Each Operation subclass represents a type of quantum operation, for example a unitary quantum gate. Each instance of these subclasses represents an application of the operation with given parameter values to a given sequence of wires (subsystems).

• Each Observable subclass represents a type of physical observable. Each instance of these subclasses represents an instruction to measure and return the respective result for the given parameter values on a sequence of wires (subsystems).

Differentiation

In general, an Operation is differentiable (at least using the finite-difference method) with respect to a parameter iff

• the domain of that parameter is continuous.

For an Operation to be differentiable with respect to a parameter using the analytic method of differentiation, it must satisfy an additional constraint:

• the parameter domain must be real.

Note

These conditions are not sufficient for analytic differentiation. For example, CV gates must also define a matrix representing their Heisenberg linear transformation on the quadrature operators.

CV Operation base classes

Due to additional requirements, continuous-variable (CV) operations must subclass the CVOperation or CVObservable classes instead of Operation and Observable.

Differentiation

To enable gradient computation using the analytic method for Gaussian CV operations, in addition, you need to provide the static class method _heisenberg_rep() that returns the Heisenberg representation of the operation given its list of parameters, namely:

• For Gaussian CV Operations this method should return the matrix of the linear transformation carried out by the operation on the vector of quadrature operators \(\mathbf{r}\) for the given parameter values.

• For Gaussian CV Observables this method should return a real vector (first-order observables) or symmetric matrix (second-order observables) of coefficients of the quadrature operators \(\x\) and \(\p\).

PennyLane uses the convention \(\mathbf{r} = (\I, \x, \p)\) for single-mode operations and observables and \(\mathbf{r} = (\I, \x_0, \p_0, \x_1, \p_1, \ldots)\) for multi-mode operations and observables.

Note

Non-Gaussian CV operations and observables are currently only supported via the finite-difference method of gradient computation.

Contents

Operator Types

Operator(*params[, wires, id])	Base class representing quantum operators.
Operation(*params[, wires, id])	Base class representing quantum gates or channels applied to quantum states.
Observable(*params[, wires, id])	Base class representing observables.
CV()	A mixin base class denoting a continuous-variable operation.
CVObservable(*params[, wires, id])	Base class representing continuous-variable observables.
CVOperation(*params[, wires, id])	Base class representing continuous-variable quantum gates.
Channel(*params[, wires, id])	Base class for quantum channels.
Tensor(*args)	Container class representing tensor products of observables.
StatePrepBase(*params[, wires, id])	An interface for state-prep operations.

Errors

When an Operator method is undefined, it raises a error type that depends on the method that is undefined.

OperatorPropertyUndefined	Generic exception to be used for undefined Operator properties or methods.
AdjointUndefinedError	Raised when an Operator's adjoint version is undefined.
DecompositionUndefinedError	Raised when an Operator's representation as a decomposition is undefined.
DiagGatesUndefinedError	Raised when an Operator's diagonalizing gates are undefined.
EigvalsUndefinedError	Raised when an Operator's eigenvalues are undefined.
GeneratorUndefinedError	Exception used to indicate that an operator does not have a generator
MatrixUndefinedError	Raised when an Operator's matrix representation is undefined.
ParameterFrequenciesUndefinedError	Exception used to indicate that an operator does not have parameter_frequencies
PowUndefinedError	Raised when an Operator's power is undefined.
SparseMatrixUndefinedError	Raised when an Operator's sparse matrix representation is undefined.
TermsUndefinedError	Raised when an Operator's representation as a linear combination is undefined.

Boolean Functions

BooleanFn’s are functions of a single object that return True or False. The operation module provides the following:

defines_diagonalizing_gates	Returns True if an operator defines the diagonalizing gates.
gen_is_multi_term_hamiltonian	Returns True if an operator has a generator defined and it is a Hamiltonian with more than one term.
has_gen	Returns True if an operator has a generator defined.
has_grad_method	Returns True if an operator has a grad_method defined.
has_multipar	Returns True if an operator has more than one parameter according to num_params.
has_nopar	Returns True if an operator has no parameters according to num_params.
has_unitary_gen	Returns True if an operator has a unitary_generator according to the has_unitary_generator flag.
is_measurement	Returns True if an operator is a MeasurementProcess instance.
is_trainable	Returns True if any of the parameters of an operator is trainable according to qml.math.requires_grad.
not_tape	Returns True if the object is not a quantum tape

Enabling New Arithmetic Operators

PennyLane is in the process of replacing Hamiltonian and Tensor with newer, more general arithmetic operators. These consist of Prod, Sum and SProd. By default, using dunder methods (eg. +, -, @, *) to combine operators with scalars or other operators will create the aforementioned newer operators. To toggle the dunders to return the older arithmetic operators, the operation module provides the following helper functions:

enable_new_opmath([warn])	Change dunder methods to return arithmetic operators instead of Hamiltonians and Tensors
disable_new_opmath([warn])	Change dunder methods to return Hamiltonians and Tensors instead of arithmetic operators
active_new_opmath()	Function that checks if the new arithmetic operator dunders are active
convert_to_opmath(op)	Converts Hamiltonian and Tensor instances into arithmetic operators.
convert_to_legacy_H(op)	Converts arithmetic operators into a legacy Hamiltonian instance.

Other

operation_derivative(operation)	Calculate the derivative of an operation.
WiresEnum(value)	Integer enumeration class to represent the number of wires an operation acts on
AllWires	An enumeration which represents all wires in the subsystem.
AnyWires	An enumeration which represents any wires in the subsystem.

PennyLane also provides a function for checking the consistency and correctness of an operator instance.

assert_valid(op[, skip_pickle, ...])

Runs basic validation checks on an Operator to make sure it has been correctly defined.

Operation attributes

PennyLane contains a mechanism for storing lists of operations with similar attributes and behaviour (for example, those that are their own inverses). The attributes below are already included, and are used primarily for the purpose of compilation transforms. New attributes can be added by instantiating new Attribute objects. Please note that these objects are located in pennylane.ops.qubit.attributes, not pennylane.operation.

Attribute	Class to represent a set of operators with a certain attribute.
composable_rotations	Operations for which composing multiple copies of the operation results in an addition (or alternative accumulation) of parameters.
diagonal_in_z_basis	Operations that are diagonal in the computational basis.
has_unitary_generator	Operations that are generated by a unitary operator.
self_inverses	Operations that are their own inverses.
supports_broadcasting	Operations that support parameter broadcasting.
symmetric_over_all_wires	Operations that are the same if you exchange the order of wires.
symmetric_over_control_wires	Controlled operations that are the same if you exchange the order of all but the last (target) wire.

code/qml_operation

 

Download Python script

 

Download Notebook

 

View on GitHub