qml.measurements

Warning

Unless you are a PennyLane or plugin developer, you likely do not need to use these classes directly.

See the main measurements page for details on available measurements.

This module contains all the measurements supported by PennyLane.

Description

Measurements

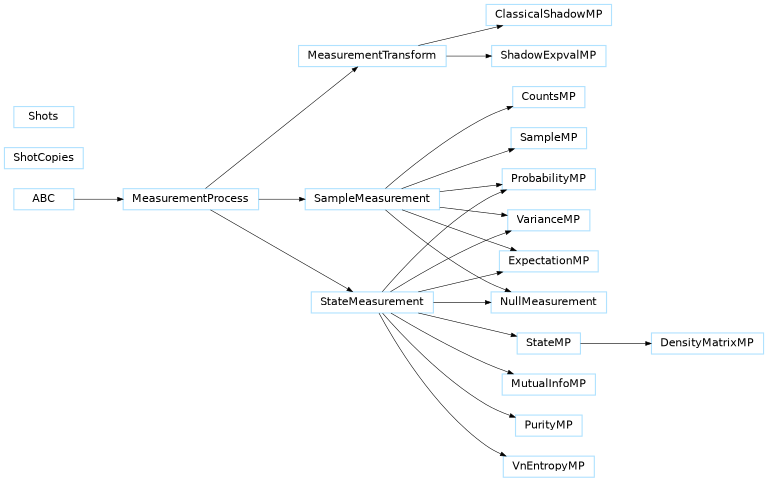
The MeasurementProcess class serves as a base class for measurements, and is inherited from by the SampleMeasurement, StateMeasurement and MeasurementTransform classes. These classes are subclassed to implement measurements in PennyLane.

• Each SampleMeasurement subclass represents a sample-based measurement, which contains a SampleMeasurement.process_samples() method and a SampleMeasurement.process_counts() method that process the sequence of samples generated by the device. process_samples method should always have the same arguments:

  • samples (Sequence[complex]): computational basis samples generated for all wires

  • wire_order (Wires): wires determining the subspace that samples acts on

  • shot_range (tuple[int]): 2-tuple of integers specifying the range of samples to use. If not specified, all samples are used.

  • bin_size (int): Divides the shot range into bins of size bin_size, and returns the measurement statistic separately over each bin. If not provided, the entire shot range is treated as a single bin.

  SampleMeasurement.process_counts() is currently optional. It accepts a dictionary mapping a string representation of a basis state to an integer and a wire order.

  See CountsMP for an example.

• Each StateMeasurement subclass represents a state-based measurement, which contains a StateMeasurement.process_state() method that processes the quantum state generated by the device. This method should always have the same arguments:

  • state (Sequence[complex]): quantum state

  • wire_order (Wires): wires determining the subspace that state acts on; a matrix of dimension \(2^n\) acts on a subspace of \(n\) wires

  See StateMP for an example.

• Each MeasurementTransform subclass represents a measurement process that requires the application of a batch transform, which contains a MeasurementTransform.process() method that converts the given quantum tape into a batch of quantum tapes and executes them using the device. This method should always have the same arguments:

  • tape (QuantumTape): quantum tape to transform

  • device (Device): device used to transform the quantum tape

  The main difference between a MeasurementTransform and a batch_transform() is that a batch transform is tracked by the gradient transform, while a MeasurementTransform process isn’t.

  See ClassicalShadowMP for an example.

Note

A measurement process can inherit from both SampleMeasurement and StateMeasurement classes, defining the needed logic to process either samples or the quantum state. See VarianceMP for an example.

Differentiation

In general, a MeasurementProcess is differentiable with respect to a parameter if the domain of that parameter is continuous. When using the analytic method of differentiation the output of the measurement process must be a real scalar value for it to be differentiable.

Working with mid-circuit measurements

Mid-circuit measurements can be made using qml.measure(). The measurement value is returned by qml.measure and can be used as a condition for classical control. Moreover, multiple measurement values can be combined using arithmetic operators for more complex conditioning:

import pennylane as qml

dev = qml.device("default.qubit", wires=3)

@qml.qnode(dev)
def circ(x, y):
    qml.RX(x, wires=0)
    qml.RY(y, wires=1)

    m0 = qml.measure(0)
    m1 = qml.measure(1)
    qml.cond(~m0 & m1 == 0, qml.X)(wires=2)
    return qml.expval(qml.Z(2))

Wires can be reused as normal after making mid-circuit measurements. Moreover, a measured wire can also be reset to the \(|0 \rangle\) state by setting the reset keyword argument of qml.measure to True.

Users can also collect statistics on mid-circuit measurements along with other terminal measurements. Currently, qml.expval, qml.probs, qml.sample, qml.counts, and qml.var are supported. qml.probs, qml.sample, and qml.counts support sequences of measurement values, qml.expval and qml.var do not. Statistics of arithmetic combinations of measurement values are supported by all but qml.probs, and only as long as they are not collected in a sequence, e.g., [m1 + m2, m1 - m2] is not supported.

import pennylane as qml

dev = qml.device("default.qubit", wires=3)

@qml.qnode(dev)
def circ(x, y):
    qml.RX(x, wires=0)
    qml.RY(y, wires=1)
    m0 = qml.measure(1)
    return qml.expval(qml.Z(0)), qml.sample(m0)

QNodes can be executed as usual when collecting mid-circuit measurement statistics:

>>> circ(1.0, 2.0, shots=5)
(0.6, array([1, 1, 1, 0, 1]))

PennyLane also supports postselecting on mid-circuit measurement outcomes. To learn more, refer to the documentation of measure().

Creating custom measurements

A custom measurement process can be created by inheriting from any of the classes mentioned above.

The following is an example for a sample-based measurement that computes the number of samples obtained of a given state:

import pennylane as qml
from pennylane.measurements import SampleMeasurement

class CountState(SampleMeasurement):
    def __init__(self, state: str):
        self.state = state  # string identifying the state e.g. "0101"
        wires = list(range(len(state)))
        super().__init__(wires=wires)

    def process_samples(self, samples, wire_order, shot_range=None, bin_size=None):
        counts_mp = qml.counts(wires=self._wires)
        counts = counts_mp.process_samples(samples, wire_order, shot_range, bin_size)
        return float(counts.get(self.state, 0))

    def process_counts(self, counts, wire_order):
        return float(counts.get(self.state, 0))

    def __copy__(self):
        return CountState(state=self.state)

Note

The __copy__ method needs to be overriden when new arguments are added into the __init__ method.

The measurement process in this example uses the counts() function, which is a measurement process which returns a dictionary containing the number of times each quantum state has been sampled.

We can now execute the new measurement in a QNode. Let’s use a simple circuit so that we can verify our results mathematically.

dev = qml.device("default.qubit", wires=1, shots=10000)

@qml.qnode(dev)
def circuit(x):
    qml.RX(x, wires=0)
    return CountState(state="1")

The quantum state before the measurement will be:

\[\begin{split}\psi = R_x(\theta) \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} \cos(\theta/2) & -i\sin(\theta/2) \\ -i\sin(\theta/2) & \cos(\theta/2) \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} \cos(\theta/2) \\ -i\sin(\theta/2) \end{bmatrix}\end{split}\]

When \(\theta = 1.23\), the probability of obtaining the state \(\begin{bmatrix} 1 \\ 0 \end{bmatrix}\) is \(\sin^2(\theta/2) = 0.333\). Using 10000 shots we should obtain the excited state 3333 times approximately.

>>> circuit(1.23)
array(3303.)

Given that the measurement process returns a real scalar value, we can differentiate it using the analytic method.

We know from the previous analysis that the analytic result of the measurement process is \(r(\theta) = \text{nshots} \cdot \sin^2(\theta/2)\).

The gradient of the measurement process is \(\frac{\partial r}{\partial \theta} = \text{nshots} \sin(\theta/2) \cos(\theta/2)\).

When \(\theta = 1.23\), \(\frac{\partial r}{\partial \theta} = 4712.444\)

>>> x = qml.numpy.array(1.23, requires_grad=True)
>>> qml.grad(circuit)(x)
4715.000000000001

Note

In PennyLane we use functions to define measurements (e.g. counts()). These functions will return an instance of the corresponding measurement process (e.g. CountsMP). This decision is just for design purposes.

Serialization and Pytree format

PennyLane measurements are automatically registered as Pytrees . MeasurementProcess._flatten and MeasurementProcess._unflatten need to be overwritten if the measurement has additional metadata, such as seed or all_outcomes.

>>> H = 2.0 * qml.X(0)
>>> mp = qml.expval(H)
>>> mp._flatten()
((2.0 * X(0), None), (('wires', None),))
>>> type(mp)._unflatten(*mp._flatten())
expval(2.0 * X(0))
>>> jax.tree_util.tree_leaves(mp)
[2.0]

Adding your new measurement to PennyLane

If you want to add this new measurement to PennyLane such that other users can benefit from it, you have to make a Pull Request creating a file with the name of your measurement (e.g. state.py) and add it in pennylane/measurements/. This file should contain:

• The measurement class with the appropriate process method defined.

• A function with the same name as the created file that will be used to instantiate the measurement class.

The tests are added to a file of a similar name and location in tests/measurements/.

The class and the function need to be imported in pennylane/measurements/__init__.py. The function needs to be imported in pennylane/__init__.py.

Here are a few more tips for adding measurements:

• Choose the name carefully. Good names tell the user what the measurement is used for, or what architecture it implements. Ask yourself if a measurement of a similar name could be added soon in a different context.

• Write good docstrings. Explain what your measurement does in a clear docstring with ample examples.

You can find more about Pennylane standards in the guidelines on Documentation.

Overview

Top-level measurement functions

The measurements functions for creating standard PennyLane measurement processes are top-level imports:

classical_shadow(wires[, seed])	The classical shadow measurement protocol.
counts([op, wires, all_outcomes])	Sample from the supplied observable, with the number of shots determined from the dev.shots attribute of the corresponding device, returning the number of counts for each sample.
density_matrix(wires)	Quantum density matrix in the computational basis.
expval(op)	Expectation value of the supplied observable.
measure(wires[, reset, postselect])	Perform a mid-circuit measurement in the computational basis on the supplied qubit.
mutual_info(wires0, wires1[, log_base])	Mutual information between the subsystems prior to measurement:
probs([wires, op])	Probability of each computational basis state.
purity(wires)	The purity of the system prior to measurement.
sample([op, wires])	Sample from the supplied observable, with the number of shots determined from the dev.shots attribute of the corresponding device, returning raw samples.
shadow_expval(H[, k, seed])	Compute expectation values using classical shadows in a differentiable manner.
state()	Quantum state in the computational basis.
var(op)	Variance of the supplied observable.
vn_entropy(wires[, log_base])	Von Neumann entropy of the system prior to measurement.

Functions

find_post_processed_mcms(circuit)

Return the subset of mid-circuit measurements which are required for post-processing.

Classes

ClassicalShadowMP([wires, seed, id])	Represents a classical shadow measurement process occurring at the end of a quantum variational circuit.
CountsMP([obs, wires, eigvals, id, all_outcomes])	Measurement process that samples from the supplied observable and returns the number of counts for each sample.
DensityMatrixMP(wires[, id])	Measurement process that returns the quantum state in the computational basis.
ExpectationMP([obs, wires, eigvals, id])	Measurement process that computes the expectation value of the supplied observable.
MeasurementProcess([obs, wires, eigvals, id])	Represents a measurement process occurring at the end of a quantum variational circuit.
MeasurementTransform([obs, wires, eigvals, id])	Measurement process that applies a transform into the given quantum tape.
MeasurementValue(measurements, processing_fn)	A class representing unknown measurement outcomes in the qubit model.
MidMeasureMP([wires, reset, postselect, id])	Mid-circuit measurement.
MutualInfoMP([wires, id, log_base])	Measurement process that computes the mutual information between the provided wires.
ProbabilityMP([obs, wires, eigvals, id])	Measurement process that computes the probability of each computational basis state.
PurityMP(wires[, id])	Measurement process that computes the purity of the system prior to measurement.
SampleMP([obs, wires, eigvals, id])	Measurement process that returns the samples of a given observable.
SampleMeasurement([obs, wires, eigvals, id])	Sample-based measurement process.
ShadowExpvalMP(H[, seed, k, id])	Measures the expectation value of an operator using the classical shadow measurement process.
ShotCopies(shots, copies)	A namedtuple that represents a shot quantity being repeated some number of times.
Shots([shots])	A data class that stores shot information.
StateMP([wires, id])	Measurement process that returns the quantum state in the computational basis.
StateMeasurement([obs, wires, eigvals, id])	State-based measurement process.
VarianceMP([obs, wires, eigvals, id])	Measurement process that computes the variance of the supplied observable.
VnEntropyMP([wires, id, log_base])	Measurement process that computes the Von Neumann entropy of the system prior to measurement.

Variables

AllCounts	Enumeration class to represent the return types of an observable.
Counts	Enumeration class to represent the return types of an observable.
Expectation	Enumeration class to represent the return types of an observable.
MidMeasure	Enumeration class to represent the return types of an observable.
MutualInfo	Enumeration class to represent the return types of an observable.
Probability	Enumeration class to represent the return types of an observable.
Purity	Enumeration class to represent the return types of an observable.
Sample	Enumeration class to represent the return types of an observable.
Shadow	Enumeration class to represent the return types of an observable.
ShadowExpval	Enumeration class to represent the return types of an observable.
State	Enumeration class to represent the return types of an observable.
Variance	Enumeration class to represent the return types of an observable.
VnEntropy	Enumeration class to represent the return types of an observable.

Class Inheritance Diagram

code/qml_measurements

 

Download Python script

 

Download Notebook

 

View on GitHub