qml.qchem.excitations

excitations(electrons, orbitals, delta_sz=0, fermionic=False)

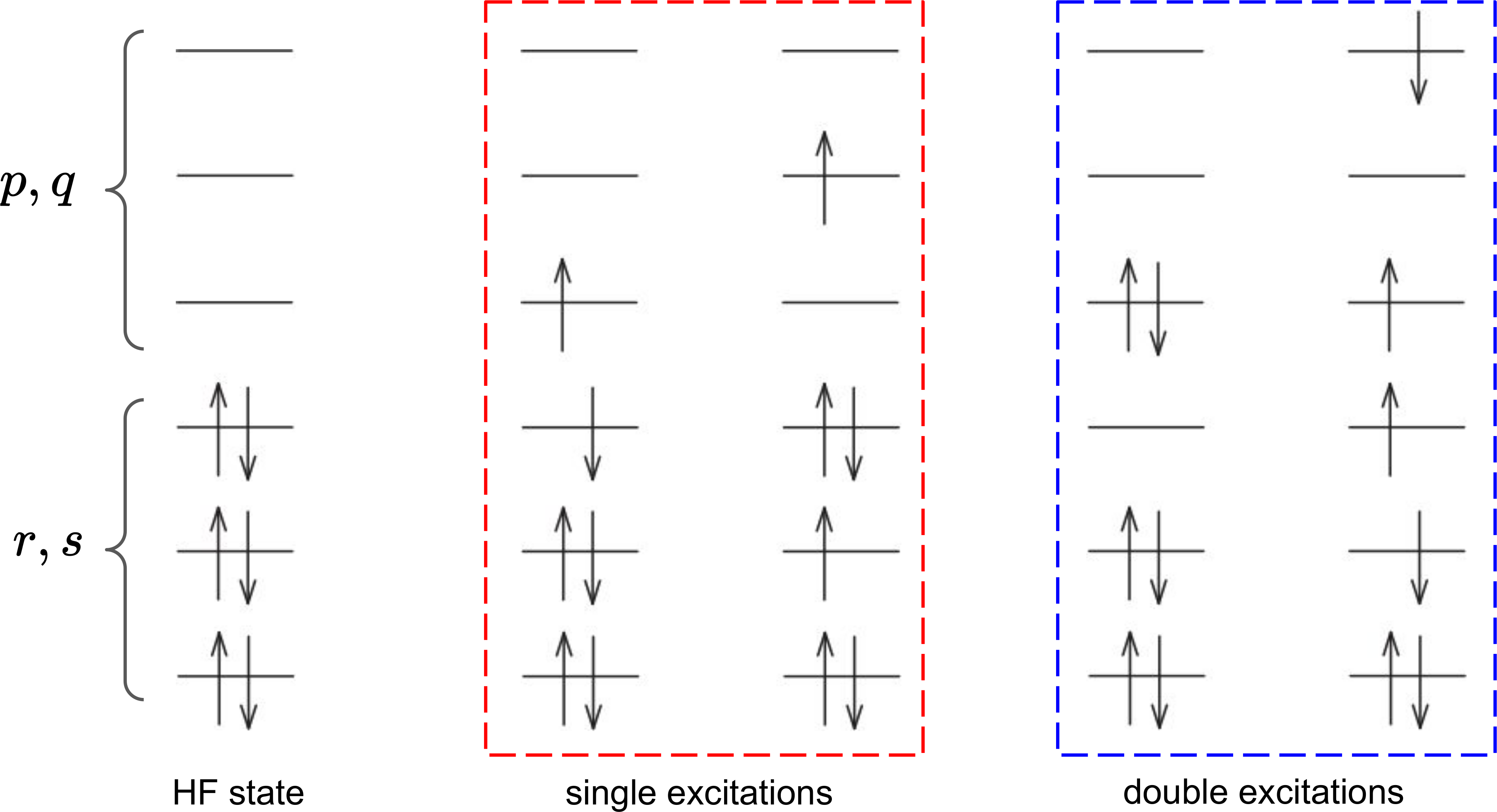
Generate single and double excitations from a Hartree-Fock reference state.

Single and double excitations can be generated by applying the operators \(\hat{T}_1\) and \(\hat{T}_2\) on the Hartree-Fock reference state:

\[\begin{split}&& \hat{T}_1 = \sum_{r \in \mathrm{occ} \\ p \in \mathrm{unocc}} \hat{c}_p^{\dagger} \hat{c}_r \\ && \hat{T}_2 = \sum_{r>s \in \mathrm{occ} \\ p>q \in \mathrm{unocc}} \hat{c}_p^{\dagger} \hat{c}_q^{\dagger} \hat{c}_r \hat{c}_s.\end{split}\]

In the equations above the indices \(r, s\) and \(p, q\) run over the occupied (occ) and unoccupied (unocc) spin orbitals and \(\hat{c}\) and \(\hat{c}^{\dagger}\) are the electron annihilation and creation operators, respectively.

Parameters:

• electrons (int) – Number of electrons. If an active space is defined, this is the number of active electrons.

• orbitals (int) – Number of spin orbitals. If an active space is defined, this is the number of active spin-orbitals.

• delta_sz (int) – Specifies the selection rules sz[p] - sz[r] = delta_sz and sz[p] + sz[p] - sz[r] - sz[s] = delta_sz for the spin-projection sz of the orbitals involved in the single and double excitations, respectively. delta_sz can take the values \(0\), \(\pm 1\) and \(\pm 2\).

• fermionic (bool) – Return a list of FermiWord objects instead of the list of orbital indices, if set to True. Default is False.

Returns:

lists with the indices of the spin orbitals involved in the single and double excitations. By default, the lists contain integers representing the orbitals, otherwise if fermionic=True they contain FermiWord objects.

Return type:

tuple(list, list)

Example

>>> electrons = 2
>>> orbitals = 4
>>> singles, doubles = excitations(electrons, orbitals)
>>> print(singles)
[[0, 2], [1, 3]]
>>> print(doubles)
[[0, 1, 2, 3]]

>>> singles, doubles = excitations(electrons, orbitals, fermionic=True)
>>> print(singles)
[FermiWord({(0, 0): '+', (1, 2): '-'}), FermiWord({(0, 1): '+', (1, 3): '-'})]
>>> print(doubles)
[FermiWord({(0, 0): '+', (1, 1): '+', (2, 2): '-', (3, 3): '-'})]

code/api/pennylane.qchem.excitations

 

Download Python script

 

Download Notebook

 

View on GitHub