qml.fourier.visualize.box

box(coeffs, n_inputs, ax, colour_dict=None, show_freqs=True, show_fliers=True)

Plot a list of sets of Fourier coefficients as a box plot.

Parameters

• coeffs (list[array[complex]]) – A list of sets of Fourier coefficients. The shape of the coefficient arrays should resemble that of the output of numpy/scipy’s fftn function, or coefficients().

• n_inputs (int) – The number of input variables in the function.

• ax (array[matplotlib.axes.Axes]) – Axis on which to plot. Must be a pair of axes from a subplot where sharex="row" and sharey="col".

• colour_dict (dict[str, str]) – A dictionary of the form {“real” : colour_string, “imag” : other_colour_string} indicating which colours should be used in the plot.

• show_freqs (bool) – Whether or not to print the frequency labels on the plot axis.

• show_fliers (bool) – Whether to display the box plot outliers.

Returns

The axes after plotting is complete.

Return type

array[matplotlib.axes.Axes]

Example

Suppose we have the following quantum function:

dev = qml.device('default.qubit', wires=2)

@qml.qnode(dev)
def circuit_with_weights(w, x):
    qml.RX(x[0], wires=0)
    qml.RY(x[1], wires=1)
    qml.CNOT(wires=[1, 0])

    qml.Rot(*w[0], wires=0)
    qml.Rot(*w[1], wires=1)
    qml.CNOT(wires=[1, 0])

    qml.RX(x[0], wires=0)
    qml.RY(x[1], wires=1)
    qml.CNOT(wires=[1, 0])

    return qml.expval(qml.Z(0))

We would like to compute and plot the distribution of Fourier coefficients for many random values of the weights w. First, we generate all the coefficients:

from functools import partial

coeffs = []

n_inputs = 2
degree = 2

for _ in range(100):
    weights = np.random.normal(0, 1, size=(2, 3))
    c = coefficients(partial(circuit_with_weights, weights), n_inputs, degree)
    coeffs.append(c)

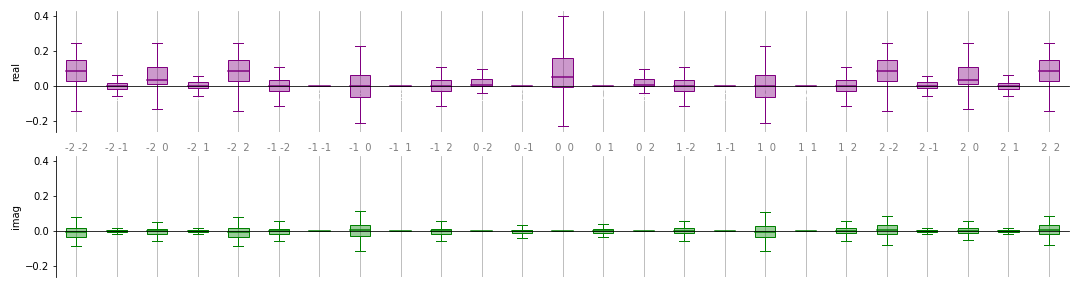
We can now plot by setting up a pair of matplotlib axes and passing them to the plotting function:

>>> import matplotlib.pyplot as plt
>>> from pennylane.fourier.visualize import box
>>> fig, ax = plt.subplots(2, 1, sharey=True, figsize=(15, 4))
>>> box(coeffs, n_inputs, ax, show_freqs=True)

code/api/pennylane.fourier.visualize.box

 

Download Python script

 

Download Notebook

 

View on GitHub