qml.IQPEmbedding¶

class IQPEmbedding(features, wires, n_repeats=1, pattern=None, id=None)[source]¶

Bases: pennylane.operation.Operation

Encodes \(n\) features into \(n\) qubits using diagonal gates of an IQP circuit.

The embedding has been proposed by Havlicek et al. (2018).

The basic IQP circuit can be repeated by specifying n_repeats. Repetitions can make the embedding “richer” through interference.

Warning

IQPEmbedding calls a circuit that involves non-trivial classical processing of the features. The features argument is therefore not differentiable when using the template, and gradients with respect to the features cannot be computed by PennyLane.

An IQP circuit is a quantum circuit of a block of Hadamards, followed by a block of gates that are diagonal in the computational basis. Here, the diagonal gates are single-qubit RZ rotations, applied to each qubit and encoding the \(n\) features, followed by two-qubit ZZ entanglers, \(e^{-i x_i x_j \sigma_z \otimes \sigma_z}\). The entangler applied to wires (wires[i], wires[j]) encodes the product of features features[i]*features[j]. The pattern in which the entanglers are applied is either the default, or a custom pattern:

If pattern is not specified, the default pattern will be used, in which the entangling gates connect all pairs of neighbours: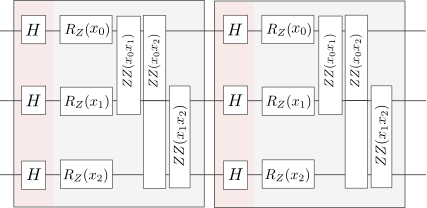
Else, pattern is a list of wire pairs [[a, b], [c, d],...], applying the entangler on wires [a, b], [c, d], etc. For example, pattern = [[0, 1], [1, 2]] produces the following entangler pattern:

Since diagonal gates commute, the order of the entanglers does not change the result.

Parameters

features (tensor_like) – tensor of features to encode
wires (Any or Iterable[Any]) – wires that the template acts on
n_repeats (int) – number of times the basic embedding is repeated
pattern (list[int]) – specifies the wires and features of the entanglers

Raises

ValueError – if inputs do not have the correct format

Usage Details

A typical usage example of the template is the following:

import pennylane as qml

dev = qml.device('default.qubit', wires=3)

@qml.qnode(dev)
def circuit(features):
    qml.IQPEmbedding(features, wires=range(3))
    return [qml.expval(qml.Z(w)) for w in range(3)]

circuit([1., 2., 3.])

Repeating the embedding

The embedding can be repeated by specifying the n_repeats argument:

@qml.qnode(dev)
def circuit(features):
    qml.IQPEmbedding(features, wires=range(3), n_repeats=4)
    return [qml.expval(qml.Z(w)) for w in range(3)]

circuit([1., 2., 3.])

Every repetition uses exactly the same quantum circuit.

Using a custom entangler pattern

A custom entangler pattern can be used by specifying the pattern argument. A pattern has to be a nested list of dimension (K, 2), where K is the number of entanglers to apply.

pattern = [[1, 2], [0, 2], [1, 0]]

@qml.qnode(dev)
def circuit(features):
    qml.IQPEmbedding(features, wires=range(3), pattern=pattern)
    return [qml.expval(qml.Z(w)) for w in range(3)]

circuit([1., 2., 3.])

Since diagonal gates commute, the order of the wire pairs has no effect on the result.

from pennylane import numpy as np

pattern1 = [[1, 2], [0, 2], [1, 0]]
pattern2 = [[1, 0], [0, 2], [1, 2]]  # a reshuffling of pattern1

@qml.qnode(dev)
def circuit(features, pattern):
    qml.IQPEmbedding(features, wires=range(3), pattern=pattern, n_repeats=3)
    return [qml.expval(qml.Z(w)) for w in range(3)]

res1 = circuit([1., 2., 3.], pattern=pattern1)
res2 = circuit([1., 2., 3.], pattern=pattern2)

assert np.allclose(res1, res2)

Non-consecutive wires

In principle, the user can also pass a non-consecutive wire list to the template. For single qubit gates, the i’th feature is applied to the i’th wire index (which may not be the i’th wire). For the entanglers, the product of i’th and j’th features is applied to the wire indices at the i’th and j’th position in wires.

For example, for wires=[2, 0, 1] the RZ block applies the first feature to wire 2, the second feature to wire 0, and the third feature to wire 1.

Likewise, using the default pattern, the entangler block applies the product of the first and second feature to the wire pair [2, 0], the product of the second and third feature to [2, 1], and so forth.

Attributes

`arithmetic_depth`	Arithmetic depth of the operator.
`basis`	The basis of an operation, or for controlled gates, of the target operation.
`batch_size`	Batch size of the operator if it is used with broadcasted parameters.
`control_wires`	Control wires of the operator.
`grad_method`
`grad_recipe`	Gradient recipe for the parameter-shift method.
`has_adjoint`
`has_decomposition`
`has_diagonalizing_gates`
`has_generator`
`has_matrix`
`has_sparse_matrix`
`hash`	Integer hash that uniquely represents the operator.
`hyperparameters`	Dictionary of non-trainable variables that this operation depends on.
`id`	Custom string to label a specific operator instance.
`is_hermitian`	This property determines if an operator is hermitian.
`name`	String for the name of the operator.
`ndim_params`	Number of dimensions per trainable parameter of the operator.
`num_params`	Number of trainable parameters that the operator depends on.
`num_wires`	Number of wires the operator acts on.
`parameter_frequencies`	Returns the frequencies for each operator parameter with respect to an expectation value of the form \(\langle \psi \| U(\mathbf{p})^\dagger \hat{O} U(\mathbf{p})\|\psi\rangle\).
`parameters`	Trainable parameters that the operator depends on.
`pauli_rep`	A `PauliSentence` representation of the Operator, or `None` if it doesn't have one.
`wires`	Wires that the operator acts on.

arithmetic_depth¶: Arithmetic depth of the operator.

basis¶

The basis of an operation, or for controlled gates, of the target operation. If not None, should take a value of "X", "Y", or "Z".

For example, X and CNOT have basis = "X", whereas ControlledPhaseShift and RZ have basis = "Z".

Type: str or None

batch_size¶

Batch size of the operator if it is used with broadcasted parameters.

The batch_size is determined based on ndim_params and the provided parameters for the operator. If (some of) the latter have an additional dimension, and this dimension has the same size for all parameters, its size is the batch size of the operator. If no parameter has an additional dimension, the batch size is None.

Returns: Size of the parameter broadcasting dimension if present, else None.
Return type: int or None

control_wires¶

Control wires of the operator.

For operations that are not controlled, this is an empty Wires object of length 0.

Returns: The control wires of the operation.
Return type: Wires

grad_method = None¶

grad_recipe = None¶

Gradient recipe for the parameter-shift method.

This is a tuple with one nested list per operation parameter. For parameter \(\phi_k\), the nested list contains elements of the form \([c_i, a_i, s_i]\) where \(i\) is the index of the term, resulting in a gradient recipe of

\[\frac{\partial}{\partial\phi_k}f = \sum_{i} c_i f(a_i \phi_k + s_i).\]

If None, the default gradient recipe containing the two terms \([c_0, a_0, s_0]=[1/2, 1, \pi/2]\) and \([c_1, a_1, s_1]=[-1/2, 1, -\pi/2]\) is assumed for every parameter.

Type: tuple(Union(list[list[float]], None)) or None

has_adjoint = False¶

has_decomposition = True¶

has_diagonalizing_gates = False¶

has_generator = False¶

has_matrix = False¶

has_sparse_matrix = False¶

hash¶

Integer hash that uniquely represents the operator.

Type: int

hyperparameters¶

Dictionary of non-trainable variables that this operation depends on.

Type: dict

id¶: Custom string to label a specific operator instance.

is_hermitian¶: This property determines if an operator is hermitian.

name¶: String for the name of the operator.

ndim_params¶

num_params¶

num_wires = -1¶: Number of wires the operator acts on.

parameter_frequencies¶

Returns the frequencies for each operator parameter with respect to an expectation value of the form \(\langle \psi | U(\mathbf{p})^\dagger \hat{O} U(\mathbf{p})|\psi\rangle\).

These frequencies encode the behaviour of the operator \(U(\mathbf{p})\) on the value of the expectation value as the parameters are modified. For more details, please see the pennylane.fourier module.

Returns: Tuple of frequencies for each parameter. Note that only non-negative frequency values are returned.
Return type: list[tuple[int or float]]

Example

>>> op = qml.CRot(0.4, 0.1, 0.3, wires=[0, 1])
>>> op.parameter_frequencies
[(0.5, 1), (0.5, 1), (0.5, 1)]

For operators that define a generator, the parameter frequencies are directly related to the eigenvalues of the generator:

>>> op = qml.ControlledPhaseShift(0.1, wires=[0, 1])
>>> op.parameter_frequencies
[(1,)]
>>> gen = qml.generator(op, format="observable")
>>> gen_eigvals = qml.eigvals(gen)
>>> qml.gradients.eigvals_to_frequencies(tuple(gen_eigvals))
(1.0,)

For more details on this relationship, see eigvals_to_frequencies().

parameters¶: Trainable parameters that the operator depends on.

pauli_rep¶: A PauliSentence representation of the Operator, or None if it doesn’t have one.

wires¶

Wires that the operator acts on.

Returns: wires
Return type: Wires

Methods

`adjoint`()	Create an operation that is the adjoint of this one.
`compute_decomposition`(features, wires, ...)	Representation of the operator as a product of other operators.
`compute_diagonalizing_gates`(*params, wires, ...)	Sequence of gates that diagonalize the operator in the computational basis (static method).
`compute_eigvals`(params, *hyperparams)	Eigenvalues of the operator in the computational basis (static method).
`compute_matrix`(params, *hyperparams)	Representation of the operator as a canonical matrix in the computational basis (static method).
`compute_sparse_matrix`(params, *hyperparams)	Representation of the operator as a sparse matrix in the computational basis (static method).
`decomposition`()	Representation of the operator as a product of other operators.
`diagonalizing_gates`()	Sequence of gates that diagonalize the operator in the computational basis.
`eigvals`()	Eigenvalues of the operator in the computational basis.
`generator`()	Generator of an operator that is in single-parameter-form.
`label`([decimals, base_label, cache])	A customizable string representation of the operator.
`map_wires`(wire_map)	Returns a copy of the current operator with its wires changed according to the given wire map.
`matrix`([wire_order])	Representation of the operator as a matrix in the computational basis.
`pow`(z)	A list of new operators equal to this one raised to the given power.
`queue`([context])	Append the operator to the Operator queue.
`simplify`()	Reduce the depth of nested operators to the minimum.
`single_qubit_rot_angles`()	The parameters required to implement a single-qubit gate as an equivalent `Rot` gate, up to a global phase.
`sparse_matrix`([wire_order])	Representation of the operator as a sparse matrix in the computational basis.
`terms`()	Representation of the operator as a linear combination of other operators.

adjoint()¶

Create an operation that is the adjoint of this one.

Adjointed operations are the conjugated and transposed version of the original operation. Adjointed ops are equivalent to the inverted operation for unitary gates.

Returns: The adjointed operation.

static compute_decomposition(features, wires, n_repeats, pattern)[source]¶

Representation of the operator as a product of other operators.

\[O = O_1 O_2 \dots O_n.\]

See also

decomposition().

Parameters

features (tensor_like) – tensor of features to encode
wires (Any or Iterable[Any]) – wires that the template acts on

Returns

decomposition of the operator

Return type

list[Operator]

Example

>>> features = torch.tensor([1., 2., 3.])
>>> pattern = [(0, 1), (0, 2), (1, 2)]
>>> qml.IQPEmbedding.compute_decomposition(features, wires=[0, 1, 2], n_repeats=2, pattern=pattern)
[Hadamard(wires=[0]), RZ(tensor(1.), wires=[0]),
 Hadamard(wires=[1]), RZ(tensor(2.), wires=[1]),
 Hadamard(wires=[2]), RZ(tensor(3.), wires=[2]),
 MultiRZ(tensor(2.), wires=[0, 1]), MultiRZ(tensor(3.), wires=[0, 2]), MultiRZ(tensor(6.), wires=[1, 2]),
 Hadamard(wires=[0]), RZ(tensor(1.), wires=[0]),
 Hadamard(wires=[1]), RZ(tensor(2.), wires=[1]),
 Hadamard(wires=[2]), RZ(tensor(3.), wires=[2]),
 MultiRZ(tensor(2.), wires=[0, 1]), MultiRZ(tensor(3.), wires=[0, 2]), MultiRZ(tensor(6.), wires=[1, 2])]

static compute_diagonalizing_gates(*params, wires, **hyperparams)¶

Sequence of gates that diagonalize the operator in the computational basis (static method).

Given the eigendecomposition \(O = U \Sigma U^{\dagger}\) where \(\Sigma\) is a diagonal matrix containing the eigenvalues, the sequence of diagonalizing gates implements the unitary \(U^{\dagger}\).

The diagonalizing gates rotate the state into the eigenbasis of the operator.

See also

diagonalizing_gates().

Parameters

params (list) – trainable parameters of the operator, as stored in the parameters attribute
wires (Iterable[Any], Wires) – wires that the operator acts on
hyperparams (dict) – non-trainable hyperparameters of the operator, as stored in the hyperparameters attribute

Returns

list of diagonalizing gates

Return type

list[Operator]

static compute_eigvals(*params, **hyperparams)¶

Eigenvalues of the operator in the computational basis (static method).

If diagonalizing_gates are specified and implement a unitary \(U^{\dagger}\), the operator can be reconstructed as

\[O = U \Sigma U^{\dagger},\]

where \(\Sigma\) is the diagonal matrix containing the eigenvalues.

Otherwise, no particular order for the eigenvalues is guaranteed.

Parameters

*params (list) – trainable parameters of the operator, as stored in the parameters attribute
**hyperparams (dict) – non-trainable hyperparameters of the operator, as stored in the hyperparameters attribute

Returns

eigenvalues

Return type

tensor_like

static compute_matrix(*params, **hyperparams)¶

Representation of the operator as a canonical matrix in the computational basis (static method).

The canonical matrix is the textbook matrix representation that does not consider wires. Implicitly, this assumes that the wires of the operator correspond to the global wire order.

See also

Operator.matrix() and qml.matrix()

Parameters

*params (list) – trainable parameters of the operator, as stored in the parameters attribute
**hyperparams (dict) – non-trainable hyperparameters of the operator, as stored in the hyperparameters attribute

Returns

matrix representation

Return type

tensor_like

static compute_sparse_matrix(*params, **hyperparams)¶

Representation of the operator as a sparse matrix in the computational basis (static method).

The canonical matrix is the textbook matrix representation that does not consider wires. Implicitly, this assumes that the wires of the operator correspond to the global wire order.

See also

sparse_matrix()

Parameters

*params (list) – trainable parameters of the operator, as stored in the parameters attribute
**hyperparams (dict) – non-trainable hyperparameters of the operator, as stored in the hyperparameters attribute

Returns

sparse matrix representation

Return type

scipy.sparse._csr.csr_matrix

decomposition()¶

Representation of the operator as a product of other operators.

\[O = O_1 O_2 \dots O_n\]

A DecompositionUndefinedError is raised if no representation by decomposition is defined.

See also

compute_decomposition().

Returns: decomposition of the operator
Return type: list[Operator]

diagonalizing_gates()¶

Sequence of gates that diagonalize the operator in the computational basis.

Given the eigendecomposition \(O = U \Sigma U^{\dagger}\) where \(\Sigma\) is a diagonal matrix containing the eigenvalues, the sequence of diagonalizing gates implements the unitary \(U^{\dagger}\).

The diagonalizing gates rotate the state into the eigenbasis of the operator.

A DiagGatesUndefinedError is raised if no representation by decomposition is defined.

See also

compute_diagonalizing_gates().

Returns: a list of operators
Return type: list[Operator] or None

eigvals()¶

Eigenvalues of the operator in the computational basis.

If diagonalizing_gates are specified and implement a unitary \(U^{\dagger}\), the operator can be reconstructed as

\[O = U \Sigma U^{\dagger},\]

where \(\Sigma\) is the diagonal matrix containing the eigenvalues.

Otherwise, no particular order for the eigenvalues is guaranteed.

Note

When eigenvalues are not explicitly defined, they are computed automatically from the matrix representation. Currently, this computation is not differentiable.

A EigvalsUndefinedError is raised if the eigenvalues have not been defined and cannot be inferred from the matrix representation.

See also

compute_eigvals()

Returns: eigenvalues
Return type: tensor_like

generator()¶

Generator of an operator that is in single-parameter-form.

For example, for operator

\[U(\phi) = e^{i\phi (0.5 Y + Z\otimes X)}\]

we get the generator

>>> U.generator()
  0.5 * Y(0) + Z(0) @ X(1)

The generator may also be provided in the form of a dense or sparse Hamiltonian (using Hamiltonian and SparseHamiltonian respectively).

The default value to return is None, indicating that the operation has no defined generator.

label(decimals=None, base_label=None, cache=None)¶

A customizable string representation of the operator.

Parameters

decimals=None (int) – If None, no parameters are included. Else, specifies how to round the parameters.
base_label=None (str) – overwrite the non-parameter component of the label
cache=None (dict) – dictionary that carries information between label calls in the same drawing

Returns

label to use in drawings

Return type

str

Example:

>>> op = qml.RX(1.23456, wires=0)
>>> op.label()
"RX"
>>> op.label(base_label="my_label")
"my_label"
>>> op = qml.RX(1.23456, wires=0, id="test_data")
>>> op.label()
"RX("test_data")"
>>> op.label(decimals=2)
"RX\n(1.23,"test_data")"
>>> op.label(base_label="my_label")
"my_label("test_data")"
>>> op.label(decimals=2, base_label="my_label")
"my_label\n(1.23,"test_data")"

If the operation has a matrix-valued parameter and a cache dictionary is provided, unique matrices will be cached in the 'matrices' key list. The label will contain the index of the matrix in the 'matrices' list.

>>> op2 = qml.QubitUnitary(np.eye(2), wires=0)
>>> cache = {'matrices': []}
>>> op2.label(cache=cache)
'U(M0)'
>>> cache['matrices']
[tensor([[1., 0.],
 [0., 1.]], requires_grad=True)]
>>> op3 = qml.QubitUnitary(np.eye(4), wires=(0,1))
>>> op3.label(cache=cache)
'U(M1)'
>>> cache['matrices']
[tensor([[1., 0.],
        [0., 1.]], requires_grad=True),
tensor([[1., 0., 0., 0.],
        [0., 1., 0., 0.],
        [0., 0., 1., 0.],
        [0., 0., 0., 1.]], requires_grad=True)]

map_wires(wire_map)[source]¶

Returns a copy of the current operator with its wires changed according to the given wire map.

Parameters: wire_map (dict) – dictionary containing the old wires as keys and the new wires as values
Returns: new operator
Return type: Operator

matrix(wire_order=None)¶

Representation of the operator as a matrix in the computational basis.

If wire_order is provided, the numerical representation considers the position of the operator’s wires in the global wire order. Otherwise, the wire order defaults to the operator’s wires.

If the matrix depends on trainable parameters, the result will be cast in the same autodifferentiation framework as the parameters.

A MatrixUndefinedError is raised if the matrix representation has not been defined.

See also

compute_matrix()

Parameters: wire_order (Iterable) – global wire order, must contain all wire labels from the operator’s wires
Returns: matrix representation
Return type: tensor_like

pow(z)¶

A list of new operators equal to this one raised to the given power.

Parameters: z (float) – exponent for the operator
Returns: list[Operator]

queue(context=<class 'pennylane.queuing.QueuingManager'>)¶: Append the operator to the Operator queue.

simplify()¶

Reduce the depth of nested operators to the minimum.

Returns: simplified operator
Return type: Operator

single_qubit_rot_angles()¶

The parameters required to implement a single-qubit gate as an equivalent Rot gate, up to a global phase.

Returns: A list of values \([\phi, \theta, \omega]\) such that \(RZ(\omega) RY(\theta) RZ(\phi)\) is equivalent to the original operation.
Return type: tuple[float, float, float]

sparse_matrix(wire_order=None)¶

Representation of the operator as a sparse matrix in the computational basis.

If wire_order is provided, the numerical representation considers the position of the operator’s wires in the global wire order. Otherwise, the wire order defaults to the operator’s wires.

A SparseMatrixUndefinedError is raised if the sparse matrix representation has not been defined.

See also

compute_sparse_matrix()

Parameters: wire_order (Iterable) – global wire order, must contain all wire labels from the operator’s wires
Returns: sparse matrix representation
Return type: scipy.sparse._csr.csr_matrix

terms()¶

Representation of the operator as a linear combination of other operators.

\[O = \sum_i c_i O_i\]

A TermsUndefinedError is raised if no representation by terms is defined.

Returns: list of coefficients \(c_i\) and list of operations \(O_i\)
Return type: tuple[list[tensor_like or float], list[Operation]]

code/api/pennylane.IQPEmbedding

Download Python script

Download Notebook

View on GitHub

qml.IQPEmbedding¶

Usage Details

Attributes

Methods

Contents

Downloads

qml.IQPEmbedding¶

Usage Details

Attributes

Methods

Contents

Downloads

Related