qml.FermionicDoubleExcitation¶
- class FermionicDoubleExcitation(weight, wires1, wires2, *, id=None)[source]¶
Bases:
OperationCircuit to exponentiate the tensor product of Pauli matrices representing the double-excitation operator entering the Unitary Coupled-Cluster Singles and Doubles (UCCSD) ansatz. UCCSD is a VQE ansatz commonly used to run quantum chemistry simulations.
The CC double-excitation operator is given by
\[\hat{U}_{pqrs}(\theta) = \mathrm{exp} \{ \theta (\hat{c}_p^\dagger \hat{c}_q^\dagger \hat{c}_r \hat{c}_s - \mathrm{H.c.}) \},\]where \(\hat{c}\) and \(\hat{c}^\dagger\) are the fermionic annihilation and creation operators and the indices \(r, s\) and \(p, q\) run over the occupied and unoccupied molecular orbitals, respectively. Using the Jordan-Wigner transformation the fermionic operator defined above can be written in terms of Pauli matrices (for more details see arXiv:1805.04340):
\[\hat{U}_{pqrs}(\theta) = \mathrm{exp} \Big\{ \frac{i\theta}{8} \bigotimes_{b=s+1}^{r-1} \hat{Z}_b \bigotimes_{a=q+1}^{p-1} \hat{Z}_a (\hat{X}_s \hat{X}_r \hat{Y}_q \hat{X}_p + \hat{Y}_s \hat{X}_r \hat{Y}_q \hat{Y}_p + \hat{X}_s \hat{Y}_r \hat{Y}_q \hat{Y}_p + \hat{X}_s \hat{X}_r \hat{X}_q \hat{Y}_p - \mathrm{H.c.} ) \Big\}\]The quantum circuit to exponentiate the tensor product of Pauli matrices entering the latter equation is shown below (see arXiv:1805.04340):
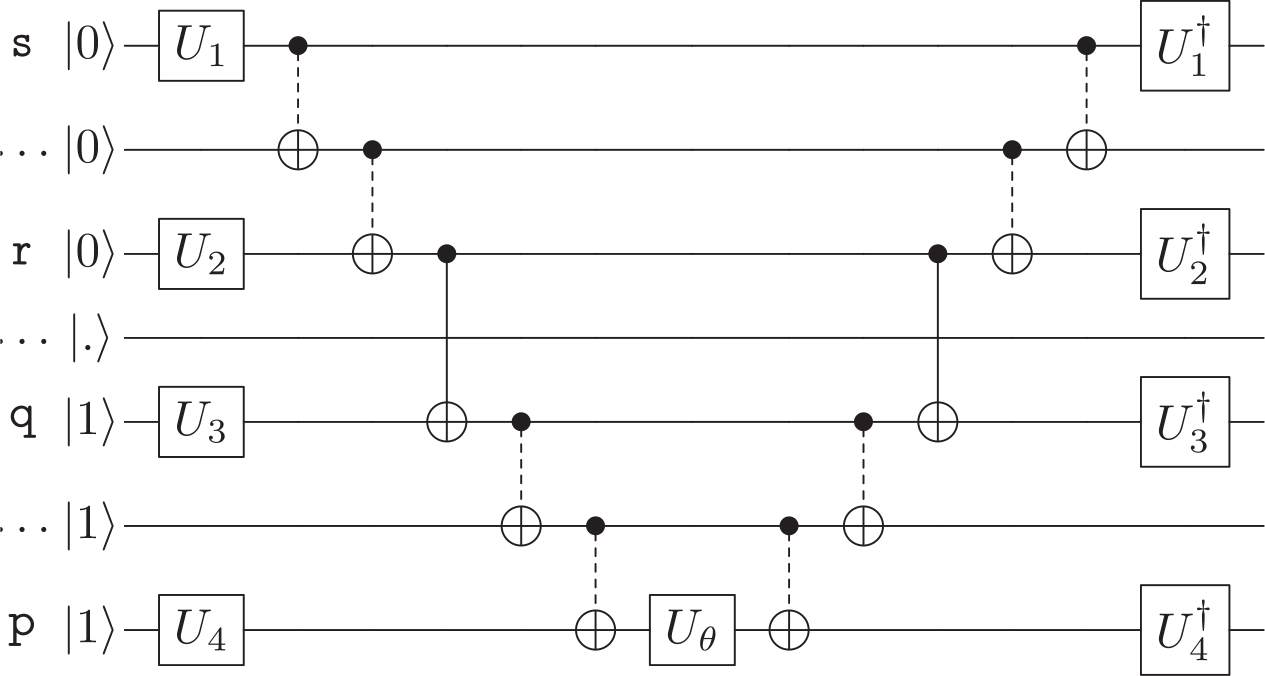
As explained in Seely et al. (2012), the exponential of a tensor product of Pauli-Z operators can be decomposed in terms of \(2(n-1)\) CNOT gates and a single-qubit Z-rotation referred to as \(U_\theta\) in the figure above. If there are \(X\) or:math:Y Pauli matrices in the product, the Hadamard (\(H\)) or \(R_x\) gate has to be applied to change to the \(X\) or \(Y\) basis, respectively. The latter operations are denoted as \(U_1\), \(U_2\), \(U_3\) and \(U_4\) in the figure above. See the Usage Details section for more details.
- Parameters:
weight (TensorLike) – angle \(\theta\) entering the Z rotation acting on wire
pwires1 (WiresLike) – Wires of the qubits representing the subset of occupied orbitals in the interval
[s, r]. The first wire is interpreted assand the last wire asr. Wires in between are acted on with CNOT gates to compute the parity of the set of qubits.wires2 (WiresLike) – Wires of the qubits representing the subset of unoccupied orbitals in the interval
[q, p]. The first wire is interpreted asqand the last wire is interpreted asp. Wires in between are acted on with CNOT gates to compute the parity of the set of qubits.
Usage Details
Notice that:
\(\hat{U}_{pqrs}(\theta)\) involves eight exponentiations where \(\hat{U}_1\), \(\hat{U}_2\), \(\hat{U}_3\), \(\hat{U}_4\) and \(\hat{U}_\theta\) are defined as follows,
\[\begin{split}[U_1, && U_2, U_3, U_4, U_{\theta}] = \\ && \Bigg\{\bigg[H, H, R_x(-\frac{\pi}{2}), H, R_z(\theta/8)\bigg], \bigg[R_x(-\frac{\pi}{2}), H, R_x(-\frac{\pi}{2}), R_x(-\frac{\pi}{2}), R_z(\frac{\theta}{8}) \bigg], \\ && \bigg[H, R_x(-\frac{\pi}{2}), R_x(-\frac{\pi}{2}), R_x(-\frac{\pi}{2}), R_z(\frac{\theta}{8}) \bigg], \bigg[H, H, H, R_x(-\frac{\pi}{2}), R_z(\frac{\theta}{8}) \bigg], \\ && \bigg[R_x(-\frac{\pi}{2}), H, H, H, R_z(-\frac{\theta}{8}) \bigg], \bigg[H, R_x(-\frac{\pi}{2}), H, H, R_z(-\frac{\theta}{8}) \bigg], \\ && \bigg[R_x(-\frac{\pi}{2}), R_x(-\frac{\pi}{2}), R_x(-\frac{\pi}{2}), H, R_z(-\frac{\theta}{8}) \bigg], \bigg[R_x(-\frac{\pi}{2}), R_x(-\frac{\pi}{2}), H, R_x(-\frac{\pi}{2}), R_z(-\frac{\theta}{8}) \bigg] \Bigg\}\end{split}\]For a given quadruple
[s, r, q, p]with \(p>q>r>s\), seventy-two single-qubit and16*(len(wires1)-1 + len(wires2)-1 + 1)CNOT operations are applied. Consecutive CNOT gates act on qubits with indices betweensandrandqandpwhile a single CNOT acts on wiresrandq. The operations performed across these qubits are shown in dashed lines in the figure above.
An example of how to use this template is shown below:
import pennylane as qml dev = qml.device('default.qubit', wires=5) @qml.qnode(dev) def circuit(weight, wires1, wires2): qml.FermionicDoubleExcitation(weight, wires1=wires1, wires2=wires2) return qml.expval(qml.Z(0)) weight = 1.34817 print(circuit(weight, wires1=[0, 1], wires2=[2, 3, 4]))
Attributes
Arithmetic depth of the operator.
The basis of an operation, or for controlled gates, of the target operation.
Batch size of the operator if it is used with broadcasted parameters.
Control wires of the operator.
Gradient recipe for the parameter-shift method.
Integer hash that uniquely represents the operator.
Dictionary of non-trainable variables that this operation depends on.
Custom string to label a specific operator instance.
This property determines if an operator is verified to be Hermitian.
This property determines if an operator is verified to be Hermitian.
String for the name of the operator.
Number of dimensions per trainable parameter of the operator.
Number of trainable parameters that the operator depends on.
Number of wires the operator acts on.
Trainable parameters that the operator depends on.
A
PauliSentencerepresentation of the Operator, orNoneif it doesn't have one.The set of parameters that affects the resource requirement of the operator.
A dictionary containing the minimal information needed to compute a resource estimate of the operator's decomposition.
Wires that the operator acts on.
- arithmetic_depth¶
Arithmetic depth of the operator.
- basis¶
The basis of an operation, or for controlled gates, of the target operation. If not
None, should take a value of"X","Y", or"Z".For example,
XandCNOThavebasis = "X", whereasControlledPhaseShiftandRZhavebasis = "Z".- Type:
str or None
- batch_size¶
Batch size of the operator if it is used with broadcasted parameters.
The
batch_sizeis determined based onndim_paramsand the provided parameters for the operator. If (some of) the latter have an additional dimension, and this dimension has the same size for all parameters, its size is the batch size of the operator. If no parameter has an additional dimension, the batch size isNone.- Returns:
Size of the parameter broadcasting dimension if present, else
None.- Return type:
int or None
- control_wires¶
Control wires of the operator.
For operations that are not controlled, this is an empty
Wiresobject of length0.- Returns:
The control wires of the operation.
- Return type:
- grad_method = 'A'¶
- grad_recipe = None¶
Gradient recipe for the parameter-shift method.
This is a tuple with one nested list per operation parameter. For parameter \(\phi_k\), the nested list contains elements of the form \([c_i, a_i, s_i]\) where \(i\) is the index of the term, resulting in a gradient recipe of
\[\frac{\partial}{\partial\phi_k}f = \sum_{i} c_i f(a_i \phi_k + s_i).\]If
None, the default gradient recipe containing the two terms \([c_0, a_0, s_0]=[1/2, 1, \pi/2]\) and \([c_1, a_1, s_1]=[-1/2, 1, -\pi/2]\) is assumed for every parameter.- Type:
tuple(Union(list[list[float]], None)) or None
- has_adjoint = False¶
- has_decomposition = True¶
- has_diagonalizing_gates = False¶
- has_generator = False¶
- has_matrix = False¶
- has_qfunc_decomposition = False¶
- has_sparse_matrix = False¶
- hash¶
Integer hash that uniquely represents the operator.
- Type:
int
- hyperparameters¶
Dictionary of non-trainable variables that this operation depends on.
- Type:
dict
- id¶
Custom string to label a specific operator instance.
- is_hermitian¶
This property determines if an operator is verified to be Hermitian.
Warning
The
is_hermitianproperty is deprecated and has been renamed tois_verified_hermitianas it better reflects the functionality of this property. The deprecated access throughis_hermitianwill be removed in PennyLane v0.45. Alternatively, consider using theis_hermitian()function instead as it provides a more reliable check for hermiticity. Please be aware that it comes with a higher computational cost.Note
This property provides a fast, non-exhaustive check used for internal optimizations. It relies on quick, provable shortcuts (e.g., operator properties) rather than a full, computationally expensive check.
For a definitive check, use the
pennylane.is_hermitian()function. Please note that this comes with increased computational cost.- Returns:
The property will return
Trueif the operator is guaranteed to be Hermitian andFalseif the check is inconclusive and the operator may or may not be Hermitian.- Return type:
bool
Consider this operator,
>>> op = (qml.X(0) @ qml.Y(0) - qml.X(0) @ qml.Z(0)) * 1j
In this case, Hermicity cannot be verified and leads to an inconclusive result:
>>> op.is_verified_hermitian # inconclusive False
However, using
pennylane.is_hermitian()will give the correct answer:>>> qml.is_hermitian(op) # definitive True
- is_verified_hermitian¶
This property determines if an operator is verified to be Hermitian.
Note
This property provides a fast, non-exhaustive check used for internal optimizations. It relies on quick, provable shortcuts (e.g., operator properties) rather than a full, computationally expensive check.
For a definitive check, use the
pennylane.is_hermitian()function. Please note that this comes with increased computational cost.- Returns:
The property will return
Trueif the operator is guaranteed to be Hermitian andFalseif the check is inconclusive and the operator may or may not be Hermitian.- Return type:
bool
Consider this operator,
>>> op = (qml.X(0) @ qml.Y(0) - qml.X(0) @ qml.Z(0)) * 1j
In this case, Hermicity cannot be verified and leads to an inconclusive result:
>>> op.is_verified_hermitian # inconclusive False
However, using
pennylane.is_hermitian()will give the correct answer:>>> qml.is_hermitian(op) # definitive True
- name¶
String for the name of the operator.
- ndim_params¶
Number of dimensions per trainable parameter of the operator.
By default, this property returns the numbers of dimensions of the parameters used for the operator creation. If the parameter sizes for an operator subclass are fixed, this property can be overwritten to return the fixed value.
- Returns:
Number of dimensions for each trainable parameter.
- Return type:
tuple
- num_params¶
- num_wires = None¶
Number of wires the operator acts on.
- parameter_frequencies = [(0.5, 1.0)]¶
- parameters¶
Trainable parameters that the operator depends on.
- pauli_rep¶
A
PauliSentencerepresentation of the Operator, orNoneif it doesn’t have one.
- resource_keys = {'num_wires_1', 'num_wires_2'}¶
The set of parameters that affects the resource requirement of the operator.
All decomposition rules for this operator class are expected to have a resource function that accepts keyword arguments that match these keys exactly. The
resource_rep()function will also expect keyword arguments that match these keys when called with this operator type.The default implementation is an empty set, which is suitable for most operators.
See also
resource_params()
- resource_params¶
Methods
adjoint()Create an operation that is the adjoint of this one.
compute_decomposition(weight, wires, wires1, ...)Representation of the operator as a product of other operators.
compute_diagonalizing_gates(*params, wires, ...)Sequence of gates that diagonalize the operator in the computational basis (static method).
compute_eigvals(*params, **hyperparams)Eigenvalues of the operator in the computational basis (static method).
compute_matrix(*params, **hyperparams)Representation of the operator as a canonical matrix in the computational basis (static method).
compute_qfunc_decomposition(*args, ...)Experimental method to compute the dynamic decomposition of the operator with program capture enabled.
compute_sparse_matrix(*params[, format])Representation of the operator as a sparse matrix in the computational basis (static method).
Representation of the operator as a product of other operators.
Sequence of gates that diagonalize the operator in the computational basis.
eigvals()Eigenvalues of the operator in the computational basis.
Generator of an operator that is in single-parameter-form.
label([decimals, base_label, cache])A customizable string representation of the operator.
map_wires(wire_map)Returns a copy of the current operator with its wires changed according to the given wire map.
matrix([wire_order])Representation of the operator as a matrix in the computational basis.
pow(z)A list of new operators equal to this one raised to the given power.
queue([context])Append the operator to the Operator queue.
simplify()Reduce the depth of nested operators to the minimum.
The parameters required to implement a single-qubit gate as an equivalent
Rotgate, up to a global phase.sparse_matrix([wire_order, format])Representation of the operator as a sparse matrix in the computational basis.
terms()Representation of the operator as a linear combination of other operators.
- adjoint()¶
Create an operation that is the adjoint of this one. Used to simplify
Adjointoperators constructed byadjoint().Adjointed operations are the conjugated and transposed version of the original operation. Adjointed ops are equivalent to the inverted operation for unitary gates.
Operator.adjointcan be optionally defined by Operator developers, whileadjoint()is the entry point for constructing generic adjoint representations.- Returns:
The adjointed operation.
>>> class MyClass(qml.operation.Operator): ... ... def adjoint(self): ... return self ... >>> op = qml.adjoint(MyClass(wires=0)) >>> op Adjoint(MyClass(wires=[0])) >>> op.decomposition() [MyClass(wires=[0])] >>> op.simplify() MyClass(wires=[0])
- static compute_decomposition(weight, wires, wires1, wires2)[source]¶
Representation of the operator as a product of other operators.
\[O = O_1 O_2 \dots O_n.\]See also
- Parameters:
weight (float or tensor_like) – angle \(\theta\) entering the Z rotation
wires (Any or Iterable[Any]) – full set of wires that the operator acts on
wires1 (Iterable) – Wires of the qubits representing the subset of occupied orbitals in the interval
[s, r].wires2 (Iterable) – Wires of the qubits representing the subset of unoccupied orbitals in the interval
[q, p].
- Returns:
decomposition of the operator
- Return type:
list[.Operator]
- static compute_diagonalizing_gates(*params, wires, **hyperparams)¶
Sequence of gates that diagonalize the operator in the computational basis (static method).
Given the eigendecomposition \(O = U \Sigma U^{\dagger}\) where \(\Sigma\) is a diagonal matrix containing the eigenvalues, the sequence of diagonalizing gates implements the unitary \(U^{\dagger}\).
The diagonalizing gates rotate the state into the eigenbasis of the operator.
See also
- Parameters:
params (list) – trainable parameters of the operator, as stored in the
parametersattributewires (Iterable[Any], Wires) – wires that the operator acts on
hyperparams (dict) – non-trainable hyperparameters of the operator, as stored in the
hyperparametersattribute
- Returns:
list of diagonalizing gates
- Return type:
list[.Operator]
- static compute_eigvals(*params, **hyperparams)¶
Eigenvalues of the operator in the computational basis (static method).
If
diagonalizing_gatesare specified and implement a unitary \(U^{\dagger}\), the operator can be reconstructed as\[O = U \Sigma U^{\dagger},\]where \(\Sigma\) is the diagonal matrix containing the eigenvalues.
Otherwise, no particular order for the eigenvalues is guaranteed.
See also
- Parameters:
*params (list) – trainable parameters of the operator, as stored in the
parametersattribute**hyperparams (dict) – non-trainable hyperparameters of the operator, as stored in the
hyperparametersattribute
- Returns:
eigenvalues
- Return type:
tensor_like
- static compute_matrix(*params, **hyperparams)¶
Representation of the operator as a canonical matrix in the computational basis (static method).
The canonical matrix is the textbook matrix representation that does not consider wires. Implicitly, this assumes that the wires of the operator correspond to the global wire order.
See also
- Parameters:
*params (list) – trainable parameters of the operator, as stored in the
parametersattribute**hyperparams (dict) – non-trainable hyperparameters of the operator, as stored in the
hyperparametersattribute
- Returns:
matrix representation
- Return type:
tensor_like
- static compute_qfunc_decomposition(*args, **hyperparameters)¶
Experimental method to compute the dynamic decomposition of the operator with program capture enabled.
When the program capture feature is enabled with
qml.capture.enable(), the decomposition of the operator is computed with this method if it is defined. Otherwise, thecompute_decomposition()method is used.The exception to this rule is when the operator is returned from the
compute_decomposition()method of another operator, in which case the decomposition is performed withcompute_decomposition()(even if this method is defined), and not with this method.When
compute_qfunc_decompositionis defined for an operator, the control flow operations within the method (specifying the decomposition of the operator) are recorded in the JAX representation.Note
This method is experimental and subject to change.
See also
- Parameters:
*args (list) – positional arguments passed to the operator, including trainable parameters and wires
**hyperparameters (dict) – non-trainable hyperparameters of the operator, as stored in the
hyperparametersattribute
- static compute_sparse_matrix(*params, format='csr', **hyperparams)¶
Representation of the operator as a sparse matrix in the computational basis (static method).
The canonical matrix is the textbook matrix representation that does not consider wires. Implicitly, this assumes that the wires of the operator correspond to the global wire order.
See also
- Parameters:
*params (list) – trainable parameters of the operator, as stored in the
parametersattributeformat (str) – format of the returned scipy sparse matrix, for example ‘csr’
**hyperparams (dict) – non-trainable hyperparameters of the operator, as stored in the
hyperparametersattribute
- Returns:
sparse matrix representation
- Return type:
scipy.sparse._csr.csr_matrix
- decomposition()¶
Representation of the operator as a product of other operators.
\[O = O_1 O_2 \dots O_n\]A
DecompositionUndefinedErroris raised if no representation by decomposition is defined.See also
- Returns:
decomposition of the operator
- Return type:
list[Operator]
- diagonalizing_gates()¶
Sequence of gates that diagonalize the operator in the computational basis.
Given the eigendecomposition \(O = U \Sigma U^{\dagger}\) where \(\Sigma\) is a diagonal matrix containing the eigenvalues, the sequence of diagonalizing gates implements the unitary \(U^{\dagger}\).
The diagonalizing gates rotate the state into the eigenbasis of the operator.
A
DiagGatesUndefinedErroris raised if no representation by decomposition is defined.See also
- Returns:
a list of operators
- Return type:
list[.Operator] or None
- eigvals()¶
Eigenvalues of the operator in the computational basis.
If
diagonalizing_gatesare specified and implement a unitary \(U^{\dagger}\), the operator can be reconstructed as\[O = U \Sigma U^{\dagger},\]where \(\Sigma\) is the diagonal matrix containing the eigenvalues.
Otherwise, no particular order for the eigenvalues is guaranteed.
Note
When eigenvalues are not explicitly defined, they are computed automatically from the matrix representation. Currently, this computation is not differentiable.
A
EigvalsUndefinedErroris raised if the eigenvalues have not been defined and cannot be inferred from the matrix representation.See also
- Returns:
eigenvalues
- Return type:
tensor_like
- generator()¶
Generator of an operator that is in single-parameter-form.
For example, for operator
\[U(\phi) = e^{i\phi (0.5 Y + Z\otimes X)}\]we get the generator
>>> U.generator() 0.5 * Y(0) + Z(0) @ X(1)
The generator may also be provided in the form of a dense or sparse Hamiltonian (using
LinearCombinationandSparseHamiltonianrespectively).
- label(decimals=None, base_label=None, cache=None)¶
A customizable string representation of the operator.
- Parameters:
decimals=None (int) – If
None, no parameters are included. Else, specifies how to round the parameters.base_label=None (str) – overwrite the non-parameter component of the label
cache=None (dict) – dictionary that carries information between label calls in the same drawing
- Returns:
label to use in drawings
- Return type:
str
Example:
>>> op = qml.RX(1.23456, wires=0) >>> op.label() 'RX' >>> op.label(base_label="my_label") 'my_label' >>> op = qml.RX(1.23456, wires=0, id="test_data") >>> op.label() 'RX\n("test_data")' >>> op.label(decimals=2) 'RX\n(1.23,"test_data")' >>> op.label(base_label="my_label") 'my_label\n("test_data")' >>> op.label(decimals=2, base_label="my_label") 'my_label\n(1.23,"test_data")'
If the operation has a matrix-valued parameter and a cache dictionary is provided, unique matrices will be cached in the
'matrices'key list. The label will contain the index of the matrix in the'matrices'list.>>> op2 = qml.QubitUnitary(np.eye(2), wires=0) >>> cache = {'matrices': []} >>> op2.label(cache=cache) 'U\n(M0)' >>> cache['matrices'] [tensor([[1., 0.], [0., 1.]], requires_grad=True)] >>> op3 = qml.QubitUnitary(np.eye(4), wires=(0,1)) >>> op3.label(cache=cache) 'U\n(M1)' >>> cache['matrices'] [tensor([[1., 0.], [0., 1.]], requires_grad=True), tensor([[1., 0., 0., 0.], [0., 1., 0., 0.], [0., 0., 1., 0.], [0., 0., 0., 1.]], requires_grad=True)]
- map_wires(wire_map)[source]¶
Returns a copy of the current operator with its wires changed according to the given wire map.
- Parameters:
wire_map (dict) – dictionary containing the old wires as keys and the new wires as values
- Returns:
new operator
- Return type:
.Operator
- matrix(wire_order=None)¶
Representation of the operator as a matrix in the computational basis.
If
wire_orderis provided, the numerical representation considers the position of the operator’s wires in the global wire order. Otherwise, the wire order defaults to the operator’s wires.If the matrix depends on trainable parameters, the result will be cast in the same autodifferentiation framework as the parameters.
A
MatrixUndefinedErroris raised if the matrix representation has not been defined.See also
- Parameters:
wire_order (Iterable) – global wire order, must contain all wire labels from the operator’s wires
- Returns:
matrix representation
- Return type:
tensor_like
- pow(z)¶
A list of new operators equal to this one raised to the given power. This method is used to simplify
Powinstances created bypow()orop ** power.Operator.powcan be optionally defined by Operator developers, whilepow()orop ** powerare the entry point for constructing generic powers to exponents.- Parameters:
z (float) – exponent for the operator
- Returns:
list[
Operator]
>>> class MyClass(qml.operation.Operator): ... ... def pow(self, z): ... return [MyClass(self.data[0]*z, self.wires)] ... >>> op = MyClass(0.5, 0) ** 2 >>> op MyClass(0.5, wires=[0])**2 >>> op.decomposition() [MyClass(1.0, wires=[0])] >>> op.simplify() MyClass(1.0, wires=[0])
- queue(context=<class 'pennylane.queuing.QueuingManager'>)¶
Append the operator to the Operator queue.
- simplify()¶
Reduce the depth of nested operators to the minimum.
- Returns:
simplified operator
- Return type:
.Operator
- single_qubit_rot_angles()¶
The parameters required to implement a single-qubit gate as an equivalent
Rotgate, up to a global phase.- Returns:
A list of values \([\phi, \theta, \omega]\) such that \(RZ(\omega) RY(\theta) RZ(\phi)\) is equivalent to the original operation.
- Return type:
tuple[float, float, float]
- sparse_matrix(wire_order=None, format='csr')¶
Representation of the operator as a sparse matrix in the computational basis.
If
wire_orderis provided, the numerical representation considers the position of the operator’s wires in the global wire order. Otherwise, the wire order defaults to the operator’s wires.A
SparseMatrixUndefinedErroris raised if the sparse matrix representation has not been defined.See also
- Parameters:
wire_order (Iterable) – global wire order, must contain all wire labels from the operator’s wires
format (str) – format of the returned scipy sparse matrix, for example ‘csr’
- Returns:
sparse matrix representation
- Return type:
scipy.sparse._csr.csr_matrix
- terms()¶
Representation of the operator as a linear combination of other operators.
\[O = \sum_i c_i O_i\]A
TermsUndefinedErroris raised if no representation by terms is defined.- Returns:
list of coefficients \(c_i\) and list of operations \(O_i\)
- Return type:
tuple[list[tensor_like or float], list[.Operation]]